PostgreSQL 中的 HyperLogLog

HyperLogLog 是一种计算近似基数计数（cardinality counting）的算法，用于解决统计唯一元素个数的问题（DISTINCT COUNT）。计算集合的确切基数需要与基数成比例的内存量，这对超大数据集来说是不切实际的。概率基数估计在理论误差范围内计算近似基数，其使用的内存要少得多，如 HyperLogLog 算法能够用 1.5kB 的内存估计大于 10^9 量级的基数，标准误差小于 2%。

HyperLogLog 是早期 LogLog 算法的扩展，LogLog 则是基于 1984 年的 Flajolet-Martin 算法发展而来。先来简单了解一下这三种算法。

Flajolet-Martin

Flajolet-Martin 算法的基本思想是利用随机化和位运算来估计唯一元素的基数。对数据集中的每个元素进行哈希映射，将元素映射为一个二进制编码。对每个哈希映射值，找到其二进制编码中从右向左的尾部连续零的个数 len，取 R 为 len 的最大值，估算基数值的公式:

2^R / ϕ (ϕ ≈ 0.77351)。

我们生成值域为 [0, 63] 之间的 8 个随机哈希值用作演示:

postgres=# select (random() * 64)::int::bit(6) from generate_series(0,7) order by 1;
  bit
--------
 000110
 001001
 010000
 011101
 011110
 101010
 110101
 111010
(8 rows)

按照 Flajolet-Martin 算法计算估算的 Cardinality:

R = 4

Cardinality: 2^4 / 0.77351 ~= 20

可以看出 Flajolet-Martin 算法的准确度较低，一个优化的方式是通过使用多个 hash 函数多次计算取平均值。

LogLog

LogLog 是 Flajolet-Martin 的改进版本，它将数据集中的元素根据哈希值分为 m 个桶，然后对每个桶分别计算 R 值，计算基数值的公式为:

m * (2^(R1 + … + Rm)/m) / ϕ (ϕ ≈ 0.77351)

用上面的随机值计算 LogLog 的 Cardinality，取 m = 4:

R1 = 1
R2 = 4
R3 = 1
R4 = 1

Cardinality: 4 * (2^(1+4+1+1)/4) / 0.77351 ~= 17

HyperLogLog

HyperLogLog 基于 LogLog 把几何平均数换成了调和平均数，其计算基数的公式为:

m * (n / (1/R1 + … + 1/Rm)) / ϕ (ϕ ≈ 0.77351, n 为不为 0 的 R 的个数)

用上面的一组值计算 HyperLogLog 的 Cardinality，取 m = 4:

R1 = 1
R2 = 4
R3 = 1
R4 = 1

Cardinality: 4 * (4 / (1/1 + 1/4 + 1/1 + 1/1)) / 0.77351 ~= 6.36

以上对 LogLog 和 HyperLogLog 的介绍从 hash 值前缀获取了 bucket id，连续 0 个数则是从后缀获得，虽然跟具体实现不一致，但不影响对算法的理解。

动态演示: Sketch of the Day: HyperLogLog

64 个 4 bits(图中绿色部分一共有15位，四个比特足够表示) 的 bucket，初始化为 0:

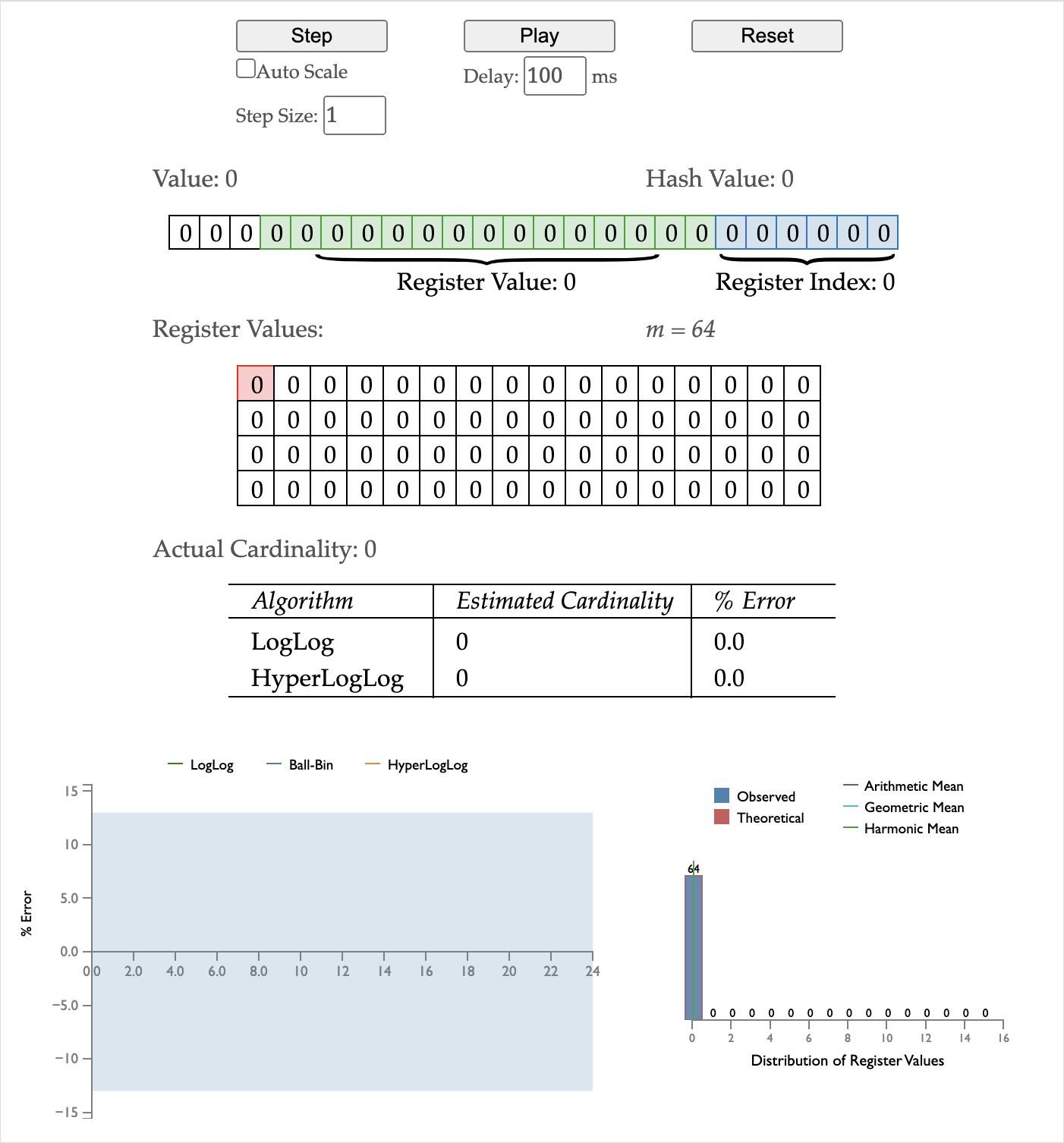
hll init

插入 4913502，其后六位代表 bucket id 为 56，取从右开始第一个 1 出现的位置（忽略 bucket 索引位），更新到对应的 bucket。

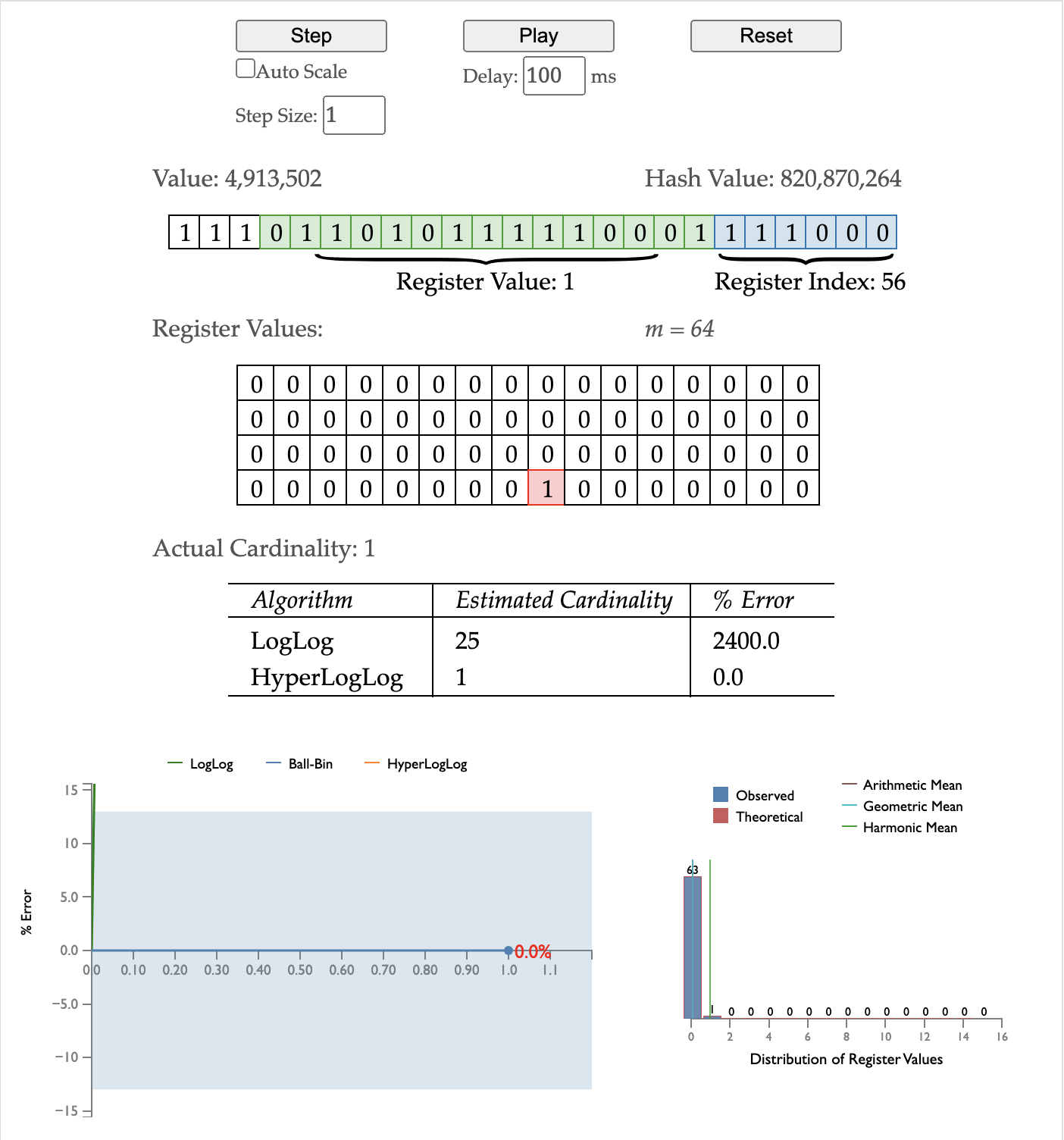
hll step 1

插入 954451，其 bucket id 为 1，第一个 1 出现的位置为 4，将其更新到对应的 bucket。

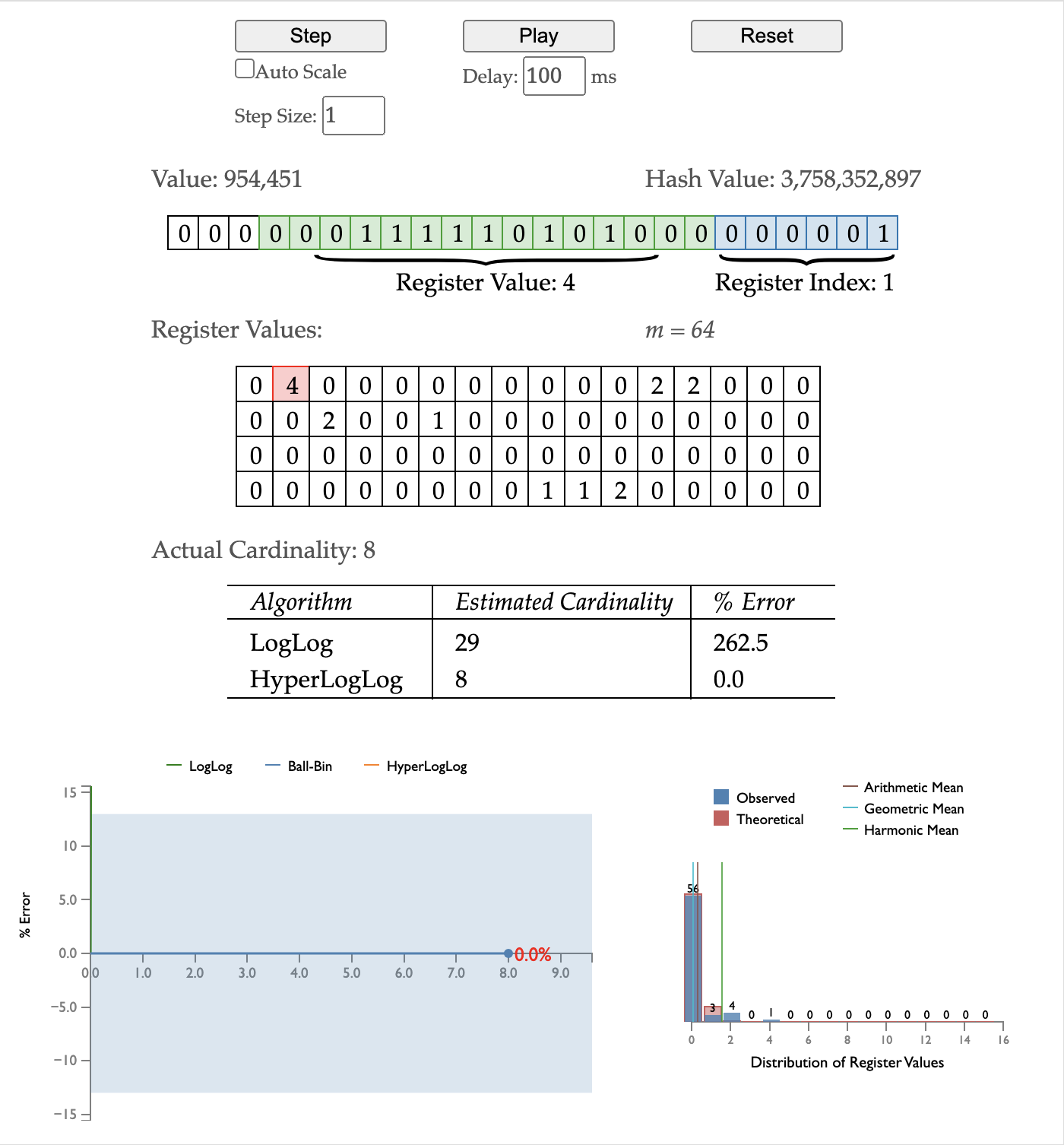
hll step 8

插入 9015653，bucket id 22 中已有的值大于新计算的值，无需更新。

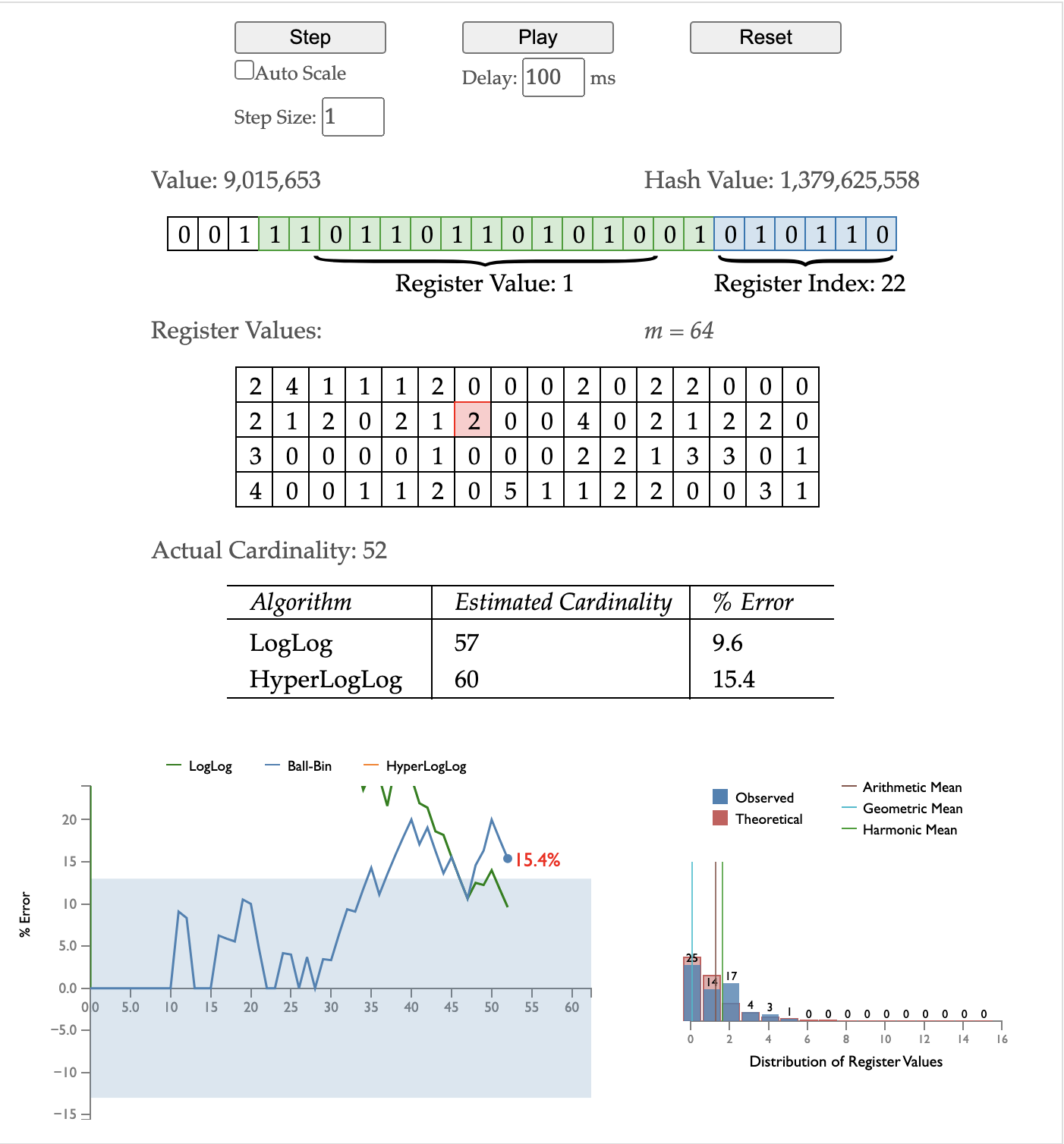
hll step 52

可以看出，HyperLogLog 的估算值大部分情况下要优于 LogLog。一些数据库和数据仓库为了支持高效的唯一计数查询，引入了 HyperLogLog 算法，如 Redis, Amazon Redshift, Presto, BigQuery 等。

postgresql-hll

PostgreSQL 本身不提供 HyperLogLog 数据结构，但可以通过 postgresql-hll 插件将 HyperLogLog 功能添加到PostgreSQL中。postgresql-hll 使用 MurmurHash3 将输入生成 64 位的哈希值。11 位 bucket index，每个 bucket 使用 5 位保存其第一个 1 出现的位置，占用空间 5 * 2^11 = 10240 bits = 1280 bytes。

postgres=# set max_parallel_workers_per_gather TO 0;
postgres=# create table dummy(id int);
CREATE TABLE
postgres=# CREATE TABLE dummyhll(set hll);
CREATE TABLE
postgres=# insert into dummy select id from generate_series(1,10000000) id order by random();
INSERT 0 10000000
postgres=# \timing
Timing is on.
postgres=# insert into dummyhll select hll_add_agg(hll_hash_integer(id)) from dummy;
INSERT 0 1
Time: 3016.966 ms (00:03.017)
postgres=# select distinct count(*) from dummy;
  count
----------
 10000000
(1 row)

Time: 1621.605 ms (00:01.622)
postgres=# explain select distinct count(*) from dummy;
                                    QUERY PLAN
----------------------------------------------------------------------------------
 Unique  (cost=169247.73..169247.74 rows=1 width=8)
   ->  Sort  (cost=169247.73..169247.74 rows=1 width=8)
         Sort Key: (count(*))
         ->  Aggregate  (cost=169247.71..169247.72 rows=1 width=8)
               ->  Seq Scan on dummy  (cost=0.00..144247.77 rows=9999977 width=0)
(5 rows)

Time: 0.584 ms
postgres=# select hll_cardinality(set) from dummyhll ;
  hll_cardinality
-------------------
 10145184.91000298
(1 row)

Time: 2.076 ms
postgres=# select pg_column_size(set) as column_size from dummyhll ;
 column_size
-------------
        1287
(1 row)

可以看出，从 hll 获取的计数值与精确基数有一定误差，但其速度却有数量级的提升。HyperLogLog 的强大之处还在于 hll 结构可以合并，这对于数据仓库的查询分析尤为重要。

PGCon 2022 的 Unconference 讨论了在 statistics 中添加 Sketches 的可能性，提到的 Apache DataSketches 也是一个非常有意思的项目。

postgresql-hll#

References#

postgresql-hll

References